Unidad 3 Distribuciones muestrales
Antes de iniciar esta sección es necesario aclarar el concepto de independencia. Para ello, consideremos dos variable aleatorias, y un evento de cada una, podemos entender la independencia como “la probabilidad de que ocurran los dos eventos al mismo tiempo es igual a la multiplicación de las probabilidades de cada evento por separado”. Además, si las variables (que definen los eventos) tienen la misma función de distribución, se dice que las variables aleatorias son independientes idénticamente distribuidas (iid).
3.1 Distribución de muestreo de la media
3.1.1 Estandarización
La estandarización, es un proceso mediante el cual los datos originales de una variable se transforman en una nueva escala que tiene una media de cero y una desviación estándar de uno. Esto permite eliminar las diferencias de escala entre las variables y facilita la comparación y el análisis estadístico (Hair et al., 2013).
Consideremos \(X\) una variable aleatoria normalmente distribuida con media \(E(X) = \mu\) y varianza \(Var(X) = \sigma^2\). El proceso de estandarización de la variable aleatoria es:
\[\begin{equation} \frac{X-\mu}{\sigma} \sim N(0,1) \tag{3.1} \end{equation}\]En el gráfico 3.1 se observa una ejemplificación de la estandarización. Al estandarizar el punto más alto de la curva se centra al rededor del 0, a su vez que la curva se angosta.
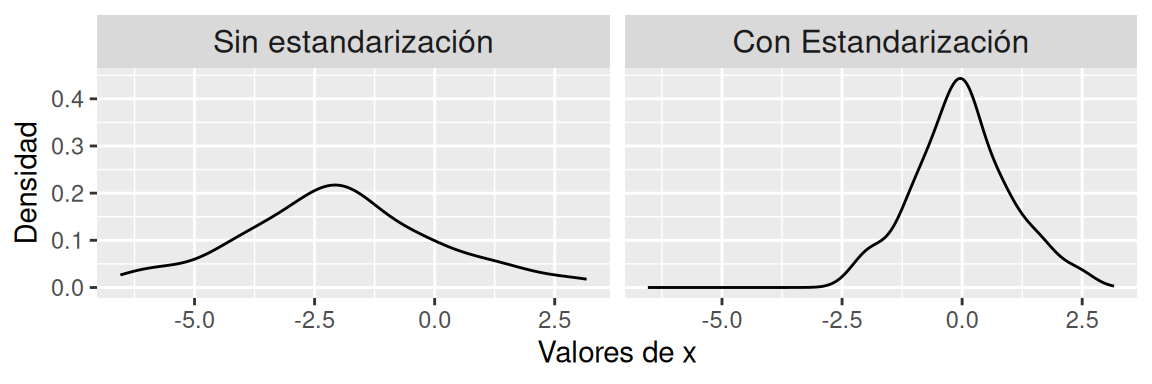
Figura 3.1: Estandarización de una variable con distribución Normal
3.1.2 Distribución de la media
Una de las medidas de resumen más importantes es la media (o promedio) de un conjunto de variables aleatorias independientes e idénticamente distribuidas.
Consideremos \(X_1, \ldots , X_n\) un conjunto de \(n\) variables aleatorias (iid), tales que, \(E(X_i) = \mu\) y \(Var(X_i) = \sigma^2\).
Entonces el estadístico
\[\begin{equation} \notag \bar{X} = (X_1 + \cdots + X_n)/n, \end{equation}\]se define como la media de las \(n\) variables aleatorias iid
\[\begin{equation} \notag \begin{split} E(\bar{X}) &= \mu\\ Var(\bar{X}) &= \sigma^2/n \end{split} \end{equation}\]Una extensión de lo anterior es:
Sea \(X_1, \ldots , X_n\) una conjunto de \(n\) variables aleatorias independientes normalmente distribuidas con medias \(E(X_i) = \mu_i\) y varianzas \(Var(X_i) = \sigma_i^2\) para \(i=1,\ldots,n\). Entonces la distribución de la media muestral es
\[\begin{equation} \bar{X}\sim N(\mu,\sigma^2/n) \tag{3.2} \end{equation}\]Con las propiedades mencionadas, es posible determinar la probabilidad de que ocurran determinados eventos que estén asociados al promedio, siempre y cuando las variables aleatorias tengan una distribución normal.
Ejemplo 3.1 El tipo de cambio del dólar a peso chileno cambia diariamente. Supóngase que este valor es una variable aleatoria distribuida normalmente con media $720 y desviación estándar de $10.
El gerente de finanzas de una empresa de retail a decidido reajustar mensualmente al alza todos los precios de sus productos, cuando el valor promedio del tipo de cambio del dólar sea superior a $724. Considerando, que se ha tomado una muestra aleatoria de 22 mediciones del dólar del mes anterior, determine la probabilidad de que el gerente aplique un alza en los precios en el próximo mes.
En primer lugar, corresponde plantear la probabilidad que se desea calcular con relación a la aplicación en el alza de precios. En este caso, la variable de estudio tiene distribución normal, por lo cual, la estandarización del promedio de la variable tiene distribución \(N(\mu = 0, \sigma^2=1)\).
\[\begin{equation} \notag \begin{split} P(\bar{X} > 724) &= P\left(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} > \frac{724-\mu}{\sigma/\sqrt{n}}\right)\\ &= P\left(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} > \frac{724-720}{10/\sqrt{22}}\right)\\ &= P\left(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} > 1.876\right)\\ \end{split} \end{equation}\]Luego, el cálculo en R es el siguiente:
## [1] 0.03032764Finalmente, la probabilidad de que el gerente aplique un alza en los precios en el próximo mes es de 0.03.
Ejercicio 3.1 La cantidad de operaciones bancarias que ocurren durante un día distribuye normal con media 75 (millones) y varianza 144 (millones). Considerando una muestra de tamaño 22 (días), ¿cuál es la probabilidad de que la media muestral de la cantidad de transacciones sea menor a 77.3 millones?
Ejercicio 3.2 El tiempo que demoran en hacerse efectivas las transferencias bancarias internacionales, distribuye normal con media 15 (segundos) y desviación estándar de 4 (segundos). Considerando una muestra de tamaño 29, ¿cuál es la probabilidad de que la media muestral de los tiempos de demora de transacción sea menor a 14.1 segundos? Mencione con rigurosidad todos los pasos de su solución.
3.1.3 Teorema del Límite Central
Considerando el ejemplo 3.1, ¿qué sucede cuándo la variable aleatoria del experimento no sigue una distribución normal? Para estos casos se utiliza el Teorema del Límite Central (TLC) (Devore, 2008, página 215).
- Anteriormente:
- (Condición) Las variables aleatorias del problema deben distribuir normal (iid).
- (Resultado) Al estandarizar el promedio, este se transforma en una variable aleatoria normal con media 0 y varianza 1.
- Con TLC:
- Se desconoce si las variable aleatorias del problema distribuyen normal (iid).
- (Condición) La cantidad de datos debe ser grande. Por regla general se utiliza un tamaño mayor a 30, sin embargo, no hay investigaciones o fuentes que lo confirmen (Johnson et al., 1994).
- (Resultado) Al estandarizar el promedio, este se transforma en una variable aleatoria normal con media 0 y varianza 1.
Consulte el siguiente enlace para acceder a una aplicación interactiva que permite visualizar el TLC.
Ejemplo 3.2 Un accionista piensa comprar acciones de una determinada empresa chilena de tecnología. Dado los valores del mercado, se observa que el valor promedio de las acciones (iid) es de $4000 con una desviación estándar de $700. El accionista comprará acciones solo si una muestra aleatoria de 100 valores de acciones resulta en un valor promedio mayor a $4100. ¿Cuál es la probabilidad de que el accionista invierta en la empresa chilena?
Si bien no se especifica que los valores de la acciones distribuyen normal, es posible usar el TLC para determinar la probabilidad.
El planteamiento de la probabilidad es el siguiente:
\[\begin{equation} \notag \begin{split} P(\bar{X} > 4100) &= P\left(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} > \frac{4100-\mu}{\sigma/\sqrt{n}}\right)\\ &= P\left(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} > \frac{4100 - 4000}{700/\sqrt{100}}\right)\\ &= P\left(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} > 1.428\right)\\ \end{split} \end{equation}\]El cálculo en R es el siguiente:
## [1] 0.07664593La probabilidad de que el accionista invierta en la empresa chilena es de 0.07
Ejercicio 3.3 La cantidad de operaciones bancarias que ocurren durante un día tienen una media de 75 (millones) y varianza 144 (millones). Considerando una muestra de tamaño 71 (días), y que se desconoce la distribución de los datos, ¿cuál es la probabilidad de que la media muestral de la cantidad de transacciones sea menor a 73.16 millones? Mencione con rigurosidad todos los pasos de su solución.
Ejercicio 3.4 El tiempo que demoran en hacerse efectivas las transferencias bancarias internacionales tienen una media de 15 (segundos) y desviación estándar de 4 (segundos). Considerando una muestra de tamaño 56, y que se desconoce la distribución de los datos, ¿cuál es la probabilidad de que la media muestral de los tiempos de demora de transacción sea menor a 15.8 segundos? Mencione con rigurosidad todos los pasos de su solución.
Ejercicio 3.5 Supóngase que el número de barriles de petróleo crudo que son importados diariamente es una variable aleatoria con una distribución no especificada. Si se observa la cantidad de barriles importados en 64 días, seleccionados en forma aleatoria , y si se sabe que la desviación estándar del número de barriles por día es \(\sigma = 60\), determínese la probabilidad de que la media muestral se encuentre a no más de 700 barriles del verdadero valor de barriles importados.
3.2 Distribución de muestreo de la varianza
Si la media es una de las medidas de localización más usadas, entonces, la varianza sería aquella con más uso dentro de las medidas de escala. Y al igual que la media, también existe una distribución de muestreo asociada a la varianza muestral.
Consideremos la expresión utilizada para calcular la varianza de un conjunto de datos (muestra):
\[\begin{equation} \notag S^2 = \sum_{i=1}^n\frac{(X_i-\mu)^2}{n-1} \end{equation}\]Se obtiene la siguiente propiedad. Sean \(X_1,\ldots,X_n\) una muestra aleatoria de una distribución normal con media \(\mu\) y varianza \(\sigma^2\). Entonces,
\[\begin{equation} Y=\sum_{i=1}^n\frac{(X_i-\mu)^2}{\sigma^2} = \frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1} \tag{3.3} \end{equation}\]Ejemplo 3.3 Considere una medición del índice de pobreza (porcentual) proporcionada por un instrumento computacional, en donde el interés recae en la variabilidad de la lectura. Supóngase que, con base en la experiencia, la medición es una variable aleatoria normalmente distribuida con media 14.7 y desviación estándar igual a 1.2 unidades. Si se toma una muestra aleatoria procedente del proceso de medición computacional de tamaño 25, ¿cuál es la probabilidad de que el valor de la varianza muestral del índice de pobreza sea mayor a \(1.1\) unidades?
El planteamiento de la probabilidad es el siguiente.
\[\begin{equation} \notag \begin{split} P(S^2 > 1.1) &= P\left(\frac{(n-1)S^2}{\sigma^2} > \frac{(n-1)\cdot 1.1}{\sigma^2}\right)\\ &= P\left(\frac{(n-1)S^2}{\sigma^2} > \frac{24\cdot 1.1}{1.2^2}\right)\\ &= P\left(\frac{(n-1)S^2}{\sigma^2} > 18.333\right)\\ \end{split} \end{equation}\]Considerando que esta nueva variable tiene distribución \(\chi^2_{n-1} = \chi^2_{25-1} = \chi^2_{24}\), el cálculo en R es el siguiente:
## [1] 0.7865623Finalmente, la probabilidad de que el valor de la varianza muestral del índice de pobreza sea mayor a \(1.1\) unidades cuadradas es de 0.7865.
Ejercicio 3.6 Se toma una muestra aleatoria de tamaño 67 proveniente de una población normal con desviación estándar \(\sigma =3.05\). Calcular la probabilidad de que la varianza muestral \(s^{2}\) sea como mínimo 8.21? Utilice solo una de las siguiente tablas.
| Cuantil | Probabilidad |
|---|---|
| 55.24886 | 0.1754 |
| 56.24816 | 0.2016 |
| 58.24886 | 0.2597 |
| 58.54886 | 0.2689 |
| 59.24886 | 0.2910 |
| Cuantil | Probabilidad |
|---|---|
| 55.24886 | 0.1996 |
| 56.24816 | 0.2279 |
| 58.24886 | 0.2895 |
| 58.54886 | 0.2992 |
| 59.24886 | 0.3223 |
3.3 La distribución T-Student
Hasta el momento sabemos que:
\(\displaystyle\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1)\)
\(\displaystyle\frac{nS^2}{\sigma^2}\sim \chi^2_{n}\)
Sin embargo, ¿qué sucede, cuándo no conocemos la varianza poblacional en la distribución de la media?
Para poder trabajar sobre la distribución de la media, reemplazamos la varianza poblacional por la muestral, dando origen a un nuevo estadístico:
\[\begin{equation} T = \frac{\bar{X}-\mu}{S/\sqrt{n}} \sim t_{n-1}, \tag{3.4} \end{equation}\]el cual, es un estadístico t-Student con \(n-1\) grados de libertad.
Ejemplo 3.4 El Departamento de Protección al Medio Ambiente (DPMA) asegura que, para un automóvil compacto en particular, el consumo promedio de gasolina en carretera es de 45 kilómetros por litro. Una organización independiente de consumidores adquiere uno de estos autos y lo somete a prueba con el propósito de verificar la cifra proporcionada por el DPMA. El auto recorrió una distancia de 100 kilómetros en 25 ocasiones. En cada recorrido se anotó el número de litros necesarios para realizar el viaje. Para los 25 ensayos, la desviación estándar tuvo un valor de 2.5 kilómetros por litro. Si se supone que el número de kilómetros que se recorre por litro es una variable aleatoria distribuida normalmente, ¿cuál es la probabilidad de que el promedio de kilómetros recorridos por litro sea menor al 45.2?
A diferencia de los expuesto anteriormente, no se conoce la varianza poblacional de la variable de estudio (los kilómetros por litro que rinde el automóvil), por lo tanto, corresponde utilizar el estadístico t-Student, el cual hace uso de la varianza muestral. El planteamiento de la probabilidad es el siguiente:
\[\begin{equation} \notag \begin{split} P(\bar{X} < 45.2) &= P\left(\frac{\bar{X}-\mu}{S/\sqrt{n}} < \frac{45.2-\mu}{S/\sqrt{n}}\right)\\ &= P\left(\frac{\bar{X}-\mu}{S/\sqrt{n}} < \frac{45.2 - 45}{2.5/\sqrt{25}}\right)\\ &= P\left(\frac{\bar{X}-\mu}{S/\sqrt{n}} < 0.4\right)\\ \end{split} \end{equation}\]Recordando que esta nueva variable distribuye \(t_{n-1}=t_{25-1}=t_{24}\), el cálculo en R es el siguiente:
## [1] 0.6536528la probabilidad de que el promedio de kilómetros recorridos por litro sea menor al 45.2 es de 0.6536.
Ejercicio 3.7 La base de datos dolar.csv contiene el valor del dólar observado de algunos de los días de los meses de junio y julio, tomados por el el SII. A continuación:
- Suponga que el valor del dólar distribuye \(N(\mu = 880,\sigma^2 = 50^2)\). Determine probabilidad de que el valor promedio del dólar muestral supere los $900.
- Considerando los supuestos de la pregunta 2, ¿cuál es la probabilidad de que la varianza muestral no supere los \(\$43^2\)? Obtenga el valor de la varianza muestral en R y comente los resultados.
- Si el valor del dólar distribuye \(N(880,\sigma^2)\). Determine probabilidad de que el valor promedio del dólar muestral supere los $900. Compare con lo obtenido en la pregunta 1, y comente.
- Con los mismos supuestos de la pregunta 3, determine por separado la probabilidad de que en cada mes, el valor promedio de valor del dólar muestral no supere los $890. Compare y comente.
Ejercicio 3.8 El conjunto de datos diabetes.csv proviene originalmente del Instituto Nacional de Diabetes y Enfermedades Digestivas y Renales. El objetivo del conjunto de datos es estudiar de forma diagnóstica si un paciente tiene diabetes, en función de ciertas medidas de diagnóstico incluidas en el conjunto de datos. Se impusieron varias restricciones a la selección de estas instancias de una base de datos más grande. En particular, todos los pacientes aquí son mujeres de al menos 21 años de ascendencia indígena Pima. Las columnas de la base de datos con las siguientes:
- Pregnancies: Para expresar el número de embarazos.
- Glucose: Para expresar el nivel de Glucosa en sangre (mg/dL).
- BloodPressure: para expresar la medida de la presión arterial distólica (mm Hg).
- SkinThickness: Para expresar el grosor de la piel (mm).
- Insulin: para expresar el nivel de insulina en sangre (mg/dL).
- BMI: Para expresar el índice de masa corporal.
- DiabetesPedigreeFunction: Para expresar el porcentaje de Diabetes.
- Age: Para expresar la edad en años.
- Outcome: Para expresar el resultado final de tener diabetes, 1 es Sí y 0 es No.
A continuación,
- Suponiendo que la edad sigue una distribución normal con media 70 y varianza 830. ¿Cuál es la probabilidad de que una persona de la base de datos tenga más de 73 años?
- Suponiendo que el grosor de la piel sigue un distribución normal con varianza 414. ¿Cuál es la probabilidad de que la varianza de la muestra sea mayor a 406?
- Suponiendo que la presión arterial sigue un distribución normal con media 69 y varianza 880. ¿Cuál es la probabilidad de que el promedio muestral de la presión arterial sea mayor a 70?
- Responda la pregunta 3 suponiendo que desconoce la varianza poblacional.
- Responda la pregunta 3 suponiendo que desconoce la distribución de los datos.