Unidad 1 Intervalos de confianza

Las bases de datos que se trabajarán en esta unidad son las siguientes:

Imacec: Contiene los datos de los valores del Imacec mensual de distintos sectores desde enero del 2018 hasta junio del 2022. Las columnas de la base de datos son las siguientes:
- Ano: Año de medición del Imacec.
- Mes: Mes de medición del Imacec.
- Mineria: Imacec del sector de minería.
- Industria: Imacec del sector de industria.
El código para cargar la base de datos en R es:
```
datos = read.csv("https://raw.githubusercontent.com/Dfranzani/Bases-de-datos-para-cursos/main/2022-2/Estad%C3%ADstica%201/imacec.csv")
```
Control cuotas: Contiene los datos de los valores cuota de los primeros tres meses del año 2022 de las AFP Plan Vital y Provida. Las columnas de la base de datos son las siguientes:
- Plan.Vital: contiene los valores cuota en pesos de la AFP Plan Vital de un APV de fondo A.
- Provida: contiene lo valores cuota en pesos de la AFP Provida de un APV de fondo A.
El código para cargar la base de datos en R es:
```
datos = read.csv("https://raw.githubusercontent.com/Dfranzani/Bases-de-datos-para-cursos/main/2023-1/control%2Bcuotas.csv")
```

1.1 Concepto

La estimación puntual aproxima mediante un número el valor de una característica poblacional o parámetro desconocido (la altura media de los chilenos, la intención de voto a un partido en las próximas elecciones generales, el tiempo medio de ejecución de un algoritmo, el valor del reajuste del IPC del próximo año) pero no nos indica el error que se comete en dicha estimación. (Devore, 2008, página 254)

Lo razonable, en la práctica, es adjuntar junto a la estimación puntual del parámetro, un margen de error de la estimación. La construcción de dicho intervalo es el objetivo de la estimación por intervalos de confianza.

Un intervalo de confianza para un parámetro con un nivel de confianza de \(1-\alpha\) (el cual debe elegir el investigador), es un intervalo de extremos aleatorios \((L,U)\) que con probabilidad \(1-\alpha\) contiene al parámetro.

\[ P(\text{Parámetro} \in (L,U)) = 1-\alpha \]

En la estimación por intervalos de confianza partimos de una muestra \(x_1,\ldots,x_n\), de lo cuales obtenemos un un intervalo numérico. Por ejemplo, podríamos hablar de que, con una confianza del \(90\%\), la estatura media de los chilenos (parámetro poblacional) está contenida por el intervalo \((1.80, 1.84)\) metros, o , la probabilidad de que el intervalo \((1.80,1.84)\) contenga al valor real de la estatura media de los chilenos en metros es de \(0.9\).

1.2 Intervalo de confianza para una media

1.2.1 Varianza poblacional conocida

Los conceptos y propiedades básicas de los intervalos de confianza son más fáciles de introducir si primero se presta atención a un problema simple, aunque un tanto irreal. Supóngase que el parámetro de interés es una media poblacional \(\mu\) y que:

La distribución de la población es normal.
El valor de la desviación estándar poblacional \(\sigma\) es conocido.

Con frecuencia la normalidad de la distribución de la población es una suposición razonable. Sin embargo, si el valor de \(\mu\) es desconocido, no es factible que el valor de \(\sigma\) estaría disponible (el conocimiento del centro de una población en general precede a la información con respecto a la dispersión). En secciones posteriores, se desarrollarán métodos basados en suposiciones menos restrictivas. (Devore, 2008, página 254)

Se supone que las observaciones muestrales reales \(x_1,\ldots , x_n\) son el resultado de una muestra aleatoria \(X_1,\ldots , X_n\) tomada de una distribución normal con valor medio \(\mu\) y desviación estándar \(\sigma\). Los resultados de la última unidad del curso de Estadística I (Distribución de la media) implican que independientemente del tamaño de la muestra (\(n\)), la media muestral \(\bar{X}\) está normalmente distribuida con valor esperado \(\mu\) y desviación estándar \(\sigma/\sqrt{n}\). Si se estandariza el promedio se obtiene la variable normal estándar

\[\begin{equation} Z = \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \sim N(\mu = 0,\sigma^2=1) \tag{1.1} \end{equation}\]

Luego, en caso de estar interesado en construir un intervalo (bilateral) de confianza para la media con una determinada confianza, se debe plantear de la siguiente forma:

\[\begin{equation} P\left( Z_{\alpha/2} < Z < Z_{1-\alpha/2}\right) = 1-\alpha \tag{1.2} \end{equation}\]

En la expresión (1.2), \(Z_{\alpha/2}\) y \(Z_{1-\alpha/2}\) son los puntos de cortes en el eje \(X\) alrededor del 0, para los cuales, el área bajo la curva (probabilidad) de la función de densidad de la distribución normal estándar es igual a \(1-\alpha\), tal como se muestra en la figura 1.1. En este sentido, para la figura planteada, los puntos de corte se traducen en las siguientes expresiones.

\[Z_{\alpha/2} = x : P(Z \leq x) = \alpha/2\] \[Z_{1-\alpha/2} = x : P(Z \leq x) = 1-\alpha/2\]

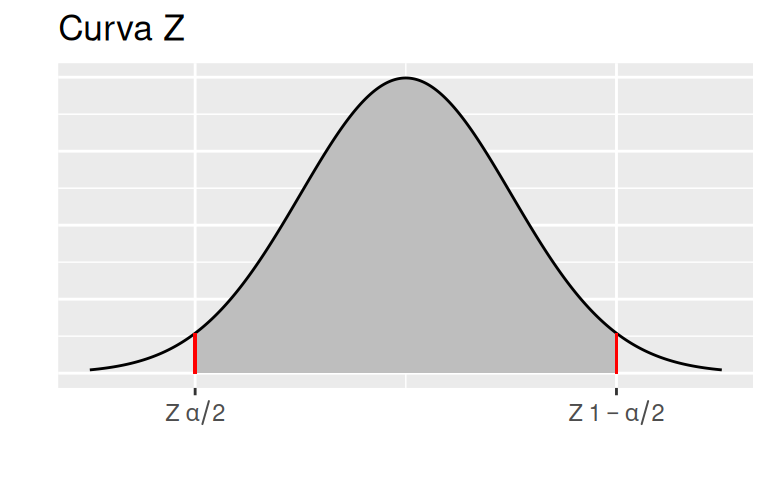
Figura 1.1: Curva Z, Normal Estándar

Luego, reemplazando el valor de \(Z\) por (1.1) en la ecuación (1.2), y despejando el valor \(\mu\) al interior de la probabilidad, se obtiene la siguiente expresión.

\[\begin{equation} P\left( \bar{X} + Z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \bar{X} + Z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\right) = 1-\alpha \tag{1.3} \end{equation}\]

\[\begin{equation} P\left( \bar{X} - Z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \bar{X} + Z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\right) = 1-\alpha \tag{1.4} \end{equation}\]

La desigualdad dentro de la probabilidad es el intervalo de confianza construido para la media poblacional, mientras que, el término a la derecha de la igualdad corresponde a la confianza trabajada por el investigador (\(1-\alpha\)).

La siguiente tabla da cuenta de las tipos de intervalo que se pueden elaborar dependiendo del tipo de estimación, es decir, un intervalo bilateral, actoado por la derecha o acotado por la izquierda.

Tabla 1.1: Intervalos de confianza para la media de una distribución normal y varianza poblacional conocida
Tipo de intervalo	Probabilidad	Expresión del intervalo
Bilateral	\(P(a < \mu < b) = 1-\alpha\)	\(\left(\bar{x} \pm Z_{1-\alpha/2}\displaystyle\frac{\sigma}{\sqrt{n}}\right)\)
Acotado por la derecha	\(P(\mu < b)=1-\alpha\)	\(\left( -\infty, \bar{x} + Z_{1-\alpha}\displaystyle\frac{\sigma}{\sqrt{n}}\right)\)
Acotado por la izquierda	\(P(a < \mu)=1-\alpha\)	\(\left(\bar{x} - Z_{1-\alpha}\displaystyle\frac{\sigma}{\sqrt{n}}, \infty\right)\)

Ejemplo 1.1 Los datos que a continuación se dan son los pesos en gramos del contenido de 16 cajas de cereal que se seleccionaron de una proceso de llenado con el propósito de verificar el peso promedio: 506, 508, 499, 503, 504, 510, 497, 512, 514, 505, 493, 496, 506, 502, 509, 496. Si el peso de cada caja es una variable aleatoria normal con una desviación estándar \(\sigma = 5g\), obtener el intervalo de confianza al 99% para la media de llenado de este proceso.

Nota: \(\bar{x} = 503.75\)

Dado que, no se especifica el tipo de intervalo, y que se está interesado es el estudiar la media del llenado de las cajas de cereal, corresponde elaborar un intervalo de confianza bilateral:

\[\left(\bar{x} \pm Z_{1-\alpha/2}\displaystyle\frac{\sigma}{\sqrt{n}}\right)\]

No existe un comando de R (nativo) para elaborar este intervalo, por lo que, la construcción debe ser manual, tal como se muestra a continuación.

peso = c(506,508,499,503,504,510,497,512,
         514,505,493,496,506,502,509,496)
promedio = mean(peso)
L = promedio - qnorm(1-0.01/2)*5/sqrt(length(peso))
U = promedio + qnorm(1-0.01/2)*5/sqrt(length(peso))
c(L,U)

## [1] 500.5302 506.9698

El resultado indica que, la probabilidad de que el intervalo \((500.5, 506.9)\) (en gramos) contenga el valor de la media de llenado de las cajas es de 0.99.

Ejercicio 1.1 Obtener los intervalos con las confianzas al 90% y 95% asociados al ejemplo 1.1. Comente las diferencias e interprete.

Dado lo expuesto en el ejercicio anterior, la figura 1.2 muestra la relación que existe entre la confianza y el rango del intervalo, en la cual, es posible observar que a mayor confianza es mayor el rango del intervalo.

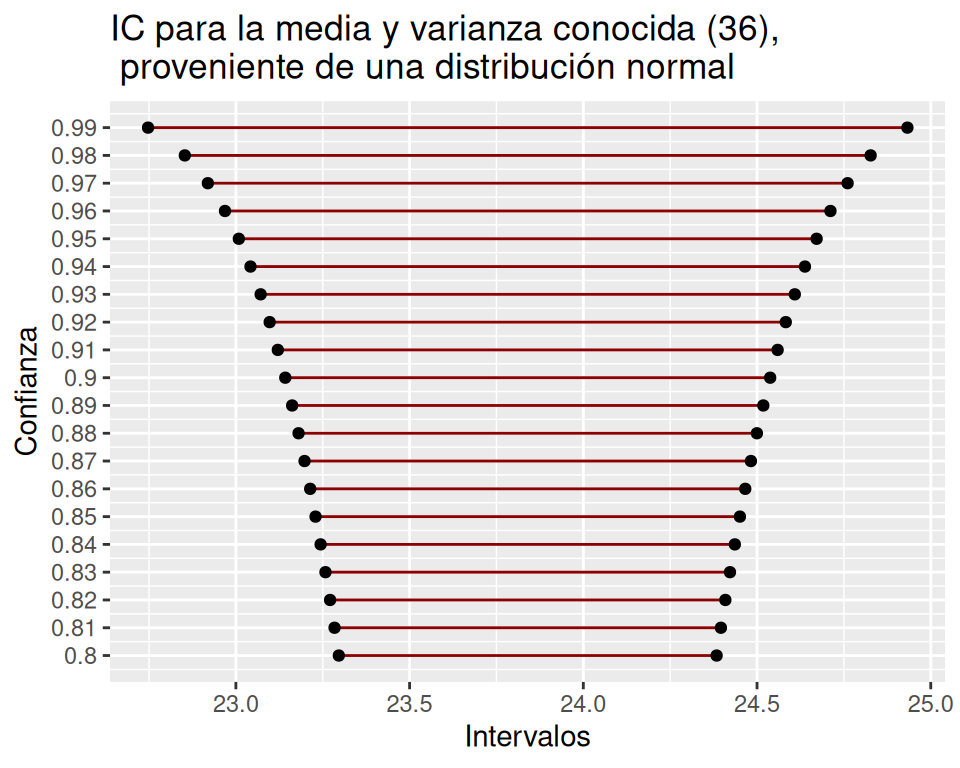
Figura 1.2: Simulación de intervalos de confianza para una media con varianza poblacional conocida

Respecto a la interpretación de los intervalos de confianza (en general, y no solo al de esta sección), si la población tiene una distribución normal, el intervalo de confianza que se obtiene con las expresiones (de la tabla anterior) es exacto. En otras palabras, si la expresión se usa repetidas veces para generar intervalos de 95% de confianza, exactamente 95% de los intervalos generados contendrán la media poblacional (Devore, 2008, página 257). El gráfico 1.3 da cuenta del fenómeno para los tres tipos de intervalos de confianza para la media con varianza poblacional desconocida; en cada tipo de intervalo se observa que la cantidad de intervalos que contiene al parámetro (color negro) es cercana a la confianza, lo cual, es más notorio al calcular una mayor cantidad de intervalos.

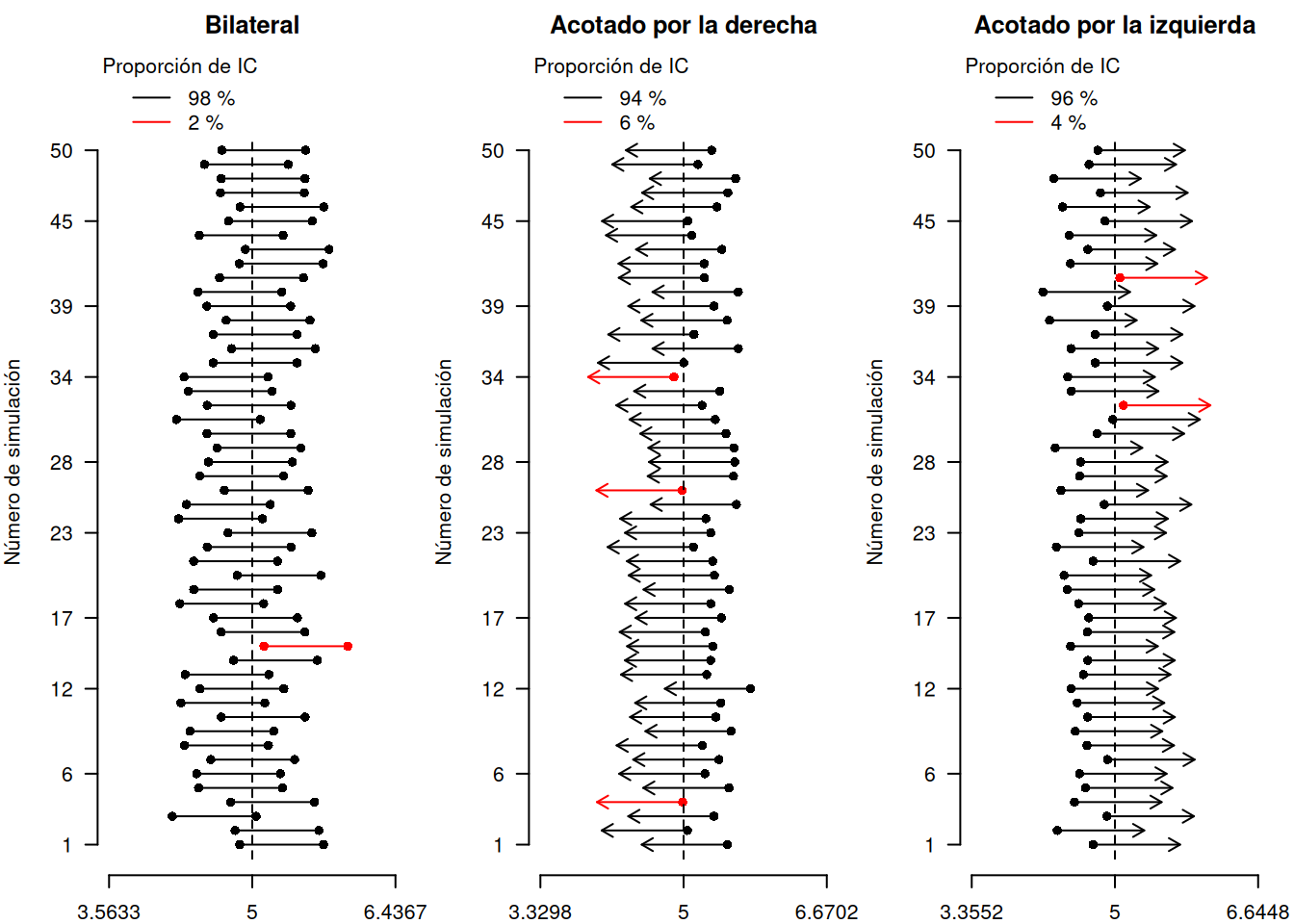
Figura 1.3: Simulación de intervalos de confianza para la media con varianza poblacional conocida

1.2.2 Varianza poblacional desconocida

Cuando se calcula un intervalo de confianza para la media poblacional, suele no contarse con una buena estimación de la desviación estándar poblacional. En tales casos se usa la misma muestra para estimar \(\mu\) y \(\sigma\). Esta situación es el caso que se conoce como \(\sigma\) desconocida. Cuando se usa \(S\) para estimar \(\sigma\), el margen de error y la estimación por intervalo de la media poblacional se basan en una distribución de probabilidad conocida como distribución \(t\). (Anderson et al., 2008, página 307)

La razón de que el número de grados de libertad para el valor de \(t\) en la tabla 1.2 sean \(n-1\) se debe al uso de \(S\) como estimación de la desviación estándar poblacional \(\sigma\). La expresión para calcular la desviación estándar muestral es:

\[ S = \sqrt{\frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})^2} \] Los grados de libertad se refieren al número de valores independientes en el cálculo de \(\sum (x_i - \bar{x})^2\). Los \(n\) valores en el cálculo de \(\sum (x_i - \bar{x})^2\) son los siguientes: \(x_1 - \bar{x},\, x_2 - \bar{x},\, \ldots,\, x_n - \bar{x}\). En estadística 1 se indicó que en cualquier conjunto de datos \(\sum (x_i - \bar{x}) = 0\). Por tanto, únicamente \(n - 1\) de los valores \(x_i - \bar{x}\) son independientes; es decir, si se conocen \(n - 1\) de estos valores, el valor restante puede determinarse exactamente usando el hecho de que los valores \(x_i - \bar{x}\) deben sumar 0. Entonces, \(n - 1\) es el número de grados de libertad en la suma \(\sum (x_i - \bar{x})^2\) y de ahí el número de grados de libertad para la distribución \(t\) en la tabla 1.2.

Tabla 1.2: Intervalos de confianza para la media de una distribución normal y varianza poblacional desconocida
Tipo de intervalo	Probabilidad	Expresión del intervalo
Bilateral	\(P(a < \mu < b) = 1-\alpha\)	\(\left(\bar{x} \pm t_{1-\alpha/2,n-1}\displaystyle\frac{S}{\sqrt{n}} \right)\)
Acotado por la derecha	\(P(\mu < b)=1-\alpha\)	\(\left( -\infty, \bar{x} + t_{1-\alpha,n-1}\displaystyle\frac{S}{\sqrt{n}}\right)\)
Acotado por la izquierda	\(P(a < \mu)=1-\alpha\)	\(\left(\bar{x} - t_{1-\alpha,n-1}\displaystyle\frac{S}{\sqrt{n}}, \infty\right)\)

Ejemplo 1.2 Para resolver el ejemplo 1.1 considerando varianza poblacional desconocida, es posible utilizar el comando t.test() para obtener el intervalo de confianza.

\[\left(\bar{x} \pm t_{1-\alpha/2,n-1}\displaystyle\frac{S}{\sqrt{n}} \right)\]

peso = c(506,508,499,503,504,510,497,512,
         514,505,493,496,506,502,509,496)
t.test(x = peso, conf.level = 0.99, alternative = "two.sided")

## 
##  One Sample t-test
## 
## data:  peso
## t = 324.89, df = 15, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 99 percent confidence interval:
##  499.181 508.319
## sample estimates:
## mean of x 
##    503.75

En este sentido, se tiene una probabilidad de 0.99 de que el intervalo \((499.1, 508.3)\) contenga el valor de la media de llenado de las cajas de cereal.

Ejercicio 1.2 Utilizando la base de datos del Imacec:

Elabore un intervalo de confianza para estudiar el valor promedio del Imacec en el sector de Minería en los años 2019 y 2021, asumiendo que el Imacec de Minería es una variable aleatoria que distribuye normal. Utilice una confianza de 91%. Interprete.
Elabore un intervalo de confianza para estudiar si, el valor promedio del Imacec en el sector de Industria en los años 2019 y 2021 es mayor a 100, asumiendo que el Imacec de Industria es una variable aleatoria que distribuye normal. Utilice una confianza de 91%. Interprete.

1.3 Intervalo de confianza para la diferencia de medias

1.3.1 Varianzas poblacionales conocidas

Sean \(\mu_X\) la media de la población X y \(\mu_Y\) la media de la población Y, lo que interesa aquí son inferencias acerca de la diferencia entre las medias: \(\mu_X - \mu_Y\). Para hacer una inferencia acerca de esta diferencia, se elige una muestra aleatoria simple de \(n_X\) unidades de la población X y otra muestra aleatoria simple de \(n_Y\) unidades de la población Y. A estas dos muestras que se toman separada e independientemente se les conoce como muestras aleatorias simples independientes.

Si ambas poblaciones tienen distribución normal o si los tamaños de las muestras son suficientemente grandes para que el teorema del límite central permita concluir que las distribuciones muestrales de \(\bar{X}\) y \(\bar{Y}\) puedan ser aproximadas mediante una distribución normal, la distribución muestral de \(\bar{X} - \bar{Y}\) tendrá una distribución normal.

En esta sección se supondrá que se cuenta con información que permite considerar que las dos desviaciones estándar \(\sigma_X\) y \(\sigma_Y\) se conocen antes de tomar las muestras. Este caso se conoce como el caso de varianzas conocidas. (Anderson et al., 2008, página 396)

Tabla 1.3: Intervalos de confianza para la diferencia de medias de dos distribucones normales y varianzas poblacionales conocidas
Tipo de intervalo	Probabilidad	Expresión del intervalo
Bilateral	\(P(a < \mu_X - \mu_Y < b) = 1-\alpha\)	\(\left(\bar{x} - \bar{y} \pm Z_{1-\alpha/2}\displaystyle\sqrt{\displaystyle\frac{\sigma^2_X}{n_x} + \displaystyle\frac{\sigma^2_Y}{n_y}}\right)\)
Acotado por la derecha	\(P(\mu_X - \mu_Y < b) = 1-\alpha\)	\(\left( -\infty, \bar{x} - \bar{y} + Z_{1-\alpha}\displaystyle\sqrt{\displaystyle\frac{\sigma^2_X}{n_x} + \displaystyle\frac{\sigma^2_Y}{n_y}}\right)\)
Acotado por la izquierda	\(P(a < \mu_X - \mu_Y) = 1-\alpha\)	\(\left(\bar{x} - \bar{y} - Z_{1-\alpha}\displaystyle\sqrt{\displaystyle\frac{\sigma^2_X}{n_x} + \displaystyle\frac{\sigma^2_Y}{n_y}}, \infty\right)\)

Ejemplo 1.3 La base de datos dolar.csv contiene los datos asociados al tipo de cambio del dólar. Las columnas de la base de datos son las siguientes:

Mes: mes de medición.
Dia: día de medición.
Valor: tipo de cambio del dólar a pesos (clp).

Elabore un intervalo de confianza para estudiar la diferencia del valor promedio del dólar entre los meses de junio y julio, asumiendo distribución normal de los datos en ambas poblaciones, y varianzas poblacionales de 1250 y 580 para cada mes respectivamente. Utilice una confianza del 95%.

Al conocer las varianzas poblacionales, y querer estudiar la diferencia, corresponde elaborar el siguiente intervalo de confianza.

\[\left(\bar{x} - \bar{y} \pm Z_{1-\alpha/2}\displaystyle\sqrt{\displaystyle\frac{\sigma^2_X}{n_x} + \displaystyle\frac{\sigma^2_Y}{n_y}}\right)\] No existe un comando en R que permita generar este intervalo de confianza, por lo que corresponde construirlo manualmente, tal como se muestra a continuación.

# Cargue previamente la base datos, guardándola con el nombre "df"
junio = df$Valor[df$Mes=="Junio"]
julio = df$Valor[df$Mes=="Julio"]
L = mean(junio) - mean(julio) - 
  qnorm(1-0.05/2)*
  sqrt(1250/length(junio) + 580/length(julio))
U = mean(junio) - mean(julio) + 
  qnorm(1-0.05/2)*
  sqrt(1250/length(junio) + 580/length(julio))
c(L,U)

## [1] -103.85536  -65.70453

El resultado indica que, la probabilidad de que el intervalo \((-103.8, -65.7)\) (en pesos) contenga al valor real de la diferencia entre ambas medias es de 0.95.

Ejercicio 1.3 Estudiar si el valor promedio del dólar de Julio es mayor al de Junio por más de 50 pesos (clp). Considere que las variables distribuyen normal, y que las varianzas poblacionales son las mismas que se mencionan en el ejemplo 1.3. Utilice una confianza del 92.3%. Interprete.

1.3.2 Varianzas poblacionales desconocidas e iguales

En esta sección el estudio de las inferencias sobre la diferencia entre dos medias poblacionales se extiende al caso en el que las dos desviaciones estándar poblacionales, \(\sigma_X\) y \(\sigma_Y\) no se conocen, además de considerar de que son iguales. En este caso, para estimar las desviaciones estándar poblacionales desconocidas se emplean las desviaciones estándar muestrales, \(S_X\) y \(S_Y\). Cuando se usan las desviaciones estándar muestrales en las estimaciones por intervalo y en las pruebas de hipótesis, se emplea la distribución \(t\) en lugar de la distribución normal estándar.

Tabla 1.4: Intervalos de confianza para la diferencia de medias de dos distribucones normales y varianzas poblacionales desconocidas e iguales
Tipo de intervalo	Probabilidad	Expresión del intervalo
Bilateral	\(P(a < \mu_X - \mu_Y < b) = 1-\alpha\)	\(\left(\bar{x} - \bar{y} \pm t_{1-\alpha/2,k}S_p\displaystyle\sqrt{\displaystyle\frac{1}{n_x} + \displaystyle\frac{1}{n_y}}\right)\)
Acotado por la derecha	\(P(\mu_X - \mu_Y < b) = 1-\alpha\)	\(\left( -\infty, \bar{x} - \bar{y} + t_{1-\alpha,k}S_p\displaystyle\sqrt{\displaystyle\frac{1}{n_x} + \displaystyle\frac{1}{n_y}}\right)\)
Acotado por la izquierda	\(P(a < \mu_X - \mu_Y) = 1-\alpha\)	\(\left(\bar{x} - \bar{y} - t_{1-\alpha,k}S_p\displaystyle\sqrt{\displaystyle\frac{1}{n_x} + \displaystyle\frac{1}{n_y}}, \infty\right)\)

donde,

\[k = n_X + n_Y-2\]

\[S_p^2 = \frac{(n_X-1)S_X^2 + (n_Y-1)S_Y^2}{n_X+n_Y-2}\]

Ejemplo 1.4 Dos universidades financiadas por el gobierno tienen métodos distintos para inscribir a sus alumnos a principios de cada semestre. Las dos desean comparar el tiempo promedio que les toma a los estudiantes el trámite de inscripción. En cada universidad se anotaron los tiempo de inscripción para 30 alumnos seleccionados al azar. Las medias y las desviaciones estándar muestrales son las siguientes:

\[\begin{equation} \notag \begin{matrix} \bar{x}_1 = 50.2 & \bar{x}_2=52.9\\ S_1 = 4.8 & S_2 = 5.4 \end{matrix} \end{equation}\]

Si se supone que el muestreo se llevó a cabo sobre dos poblaciones distribuidas normales e independientes con varianzas iguales , obtener el intervalo de confianza estimado del 99% para la diferencia entre las medias del tiempo de inscripción para las dos universidades. Con base en este evidencia, ¿se estaría inclinando a concluir que existe una diferencia real entre los tiempos medios para cada universidad?

Para responder a la pregunta, es necesario construir un intervalo de confianza para la diferencia de medias y, verificar si el cero está incluido dentro de este. El desarrollo del intervalo debe ser manual, ya que, no se cuenta con una base de datos, sino que directamente con los promedios y desviaciones estándar de las muestras.

\[\begin{equation} \notag \begin{split} &\left(\bar{x}_1 - \bar{x}_2 \pm t_{1-\alpha/2,k}S_p\displaystyle\sqrt{\displaystyle\frac{1}{n_{X_1}} + \displaystyle\frac{1}{n_{X_2}}}\right) = \left(-6.208;0.808 \right)\\ S_p^2 &= \frac{(n_{X_1}-1)S_{X_1}^2 + (n_{X_2}-1)S_{X_2}^2}{n_{X_1}+n_{X_2}-2} = \frac{29\cdot 4.8^2 + 29\cdot 5.4^2}{58} = 26.1\\ k &= n_{X_1} + n_{X_2}-2 = 58 \text{, } t_{0.995, 58} = 2.66\\ \end{split} \end{equation}\]

Como el intervalo contiene al cero, no existe suficiente evidencia para indicar que existe una diferencia real entre los tiempos medios para cada universidad, con un 99% de confianza.

Ejercicio 1.4 La base de datos Control cuotas contiene los datos de los valores cuota de los primeros tres meses del año 2022 de las AFP Plan Vital y Provida. Se está interesado en saber si el valor promedio de las cuotas de Plan Vital supera al de Provida por más de 30000 pesos, para ello, elabore un intervalo de confianza con una confianza del 90%. Asuma, que el valor cuota es una variable aleatoria que distribuye normal en ambas poblaciones (independientes), y que las varianzas poblacionales son desconocidas e iguales.

Ejercicio 1.5 Utilizando la base de datos Control cuotas, estudiar si la media del valor cuota de Provida es menor a la de Plan Vital, utilizando una confianza del 99.64% Considere distribución normal de las variables y varianzas poblacionales desconocidas e iguales.

1.3.3 Varianzas poblacionales desconocidas y distintas

A diferencia de los visto en la sección anterior, las dos desviaciones estándar poblacionales, \(\sigma_X\) y \(\sigma_Y\) si bien no se conocen, se consideran distintas.

Tabla 1.5: Intervalos de confianza para la diferencia de medias de dos distribucones normales y varianzas poblacionales desconocidas y distintas
Tipo de intervalo	Probabilidad	Expresión del intervalo
Bilateral	\(P(a < \mu_X - \mu_Y < b) = 1-\alpha\)	\(\left(\bar{x} - \bar{y} \pm t_{1-\alpha/2,k}\sqrt{S^2_X/n_X + S^2_Y/n_Y}\right)\)
Acotado por la derecha	\(P(\mu_X - \mu_Y < b) = 1-\alpha\)	\(\left( -\infty, \bar{x} - \bar{y} + t_{1-\alpha,k}\sqrt{S^2_X/n_X + S^2_Y/n_Y}\right)\)
Acotado por la izquierda	\(P(a < \mu_X - \mu_Y) = 1-\alpha\)	\(\left(\bar{x} - \bar{y} - t_{1-\alpha,k}\sqrt{S^2_X/n_X + S^2_Y/n_Y}, \infty\right)\)

dónde \(k\) es el entero más cercano a

\[\frac{(S_X^2/n_X + S_Y^2/n_Y)^2}{(S_X^2/n_X)^2/(n_X-1) + (S_Y^2/n_Y)^2/(n_Y-1)}\]

Ejemplo 1.5 Resuelva el ejemplo 1.3 asumiendo varianzas poblacionales desconocidas y diferentes.

Al asumir que las varianzas poblacionales son desconocidas y diferentes, corresponde elaborar el siguiente intervalo.

\[\left(\bar{x} - \bar{y} \pm t_{1-\alpha/2,k}\sqrt{S^2_X/n_X + S^2_Y/n_Y}\right)\]

La ejecución en R es mediante el comando t.test() considerando el argumento var.equal = F, el cual, indica que las varianzas poblacionales son desconocidas y distintas (por defecto el valor de este argumento es F, es decir, se asume que las varianzas poblacionales son desconocidas y distintas). Además, se asume una confianza del 95%.

junio = df$Valor[df$Mes=="Junio"]
julio = df$Valor[df$Mes=="Julio"]
t.test(x = junio, y = julio, conf.level = 0.95, var.equal = F)

## 
##  Welch Two Sample t-test
## 
## data:  junio and julio
## t = -8.793, df = 33.349, p-value = 3.338e-10
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -104.38837  -65.17152
## sample estimates:
## mean of x mean of y 
##  857.7695  942.5494

El resultado indica que, la probabilidad de que el intervalo \((-104.3, -65.17)\) (en pesos) contenga al valor real de la diferencia entre ambas medias es de 0.95.

Ejercicio 1.6 Utilizando la base de datos del Imacec, elabore un intervalo de confianza para estudiar si, la media del Imacec del sector de minería es menor al del sector de industria en el periodo 2019-2020. Asuma que, las distribuciones poblacionales son normales e indendientes, y que las varianzas poblacionales son desconocidas y distintas. Utilice una confianza del 96%. Interprete.

1.4 Intervalo de confianza para la comparación de varianzas

De vez en cuando se requieren métodos de comparar dos varianzas de población (o desviaciones estándar), aunque tales problemas surgen con mucho menor frecuencia que aquellos que implican medias o proporciones. Para el caso en que las poblaciones investigadas son normales, los procedimientos están basados en una nueva familia de distribuciones de probabilidad.

Distribución F

La distribución de probabilidad \(F\) tiene dos parámetros, denotados por \(\nu_{1}\) y \(\nu_{2}\). El parámetro \(\nu_{1}\) se conoce como y \(\nu_{2}\) es el ; en este caso \(\nu_{1}\) y \(\nu_{2}\) son enteros positivos. Una variable aleatoria que tiene una distribución \(F\) no puede asumir un valor negativo. Como la función de densidad es complicada y no será utilizada en forma explícita, se omite la fórmula. Existe una importante conexión entre una variable \(F\) y variables chi-cuadrado. Si \(X_{1}\) y \(X_{2}\) son variables aleatorias chi-cuadradas independientes con \(\nu_{1}\) y \(\nu_{2}\) grados de libertad, respectivamente, entonces la variable aleatoria

\[ F = \frac{X_{1}/\nu_{1}}{X_{2}/\nu_{2}} \]

se puede demostrar que la razón de las dos variables chi-cuadradas divididas entre sus respectivos grados de libertad tiene una distribución \(F\). (Devore, 2008, página 360)

En esta sección, se hará uso únicamente del intervalo bilateral, ya que, es el único tipo de intervalo que no permite determinar si las varianzas poblacionales deben ser consideradas desconocidas distintas o iguales.

\[\begin{equation} \begin{split} P\left(a<\frac{\sigma_Y^2}{\sigma_X^2}<b\right) = 1-\alpha &\Rightarrow \left( F_1\frac{S_Y^2}{S_X^2},F_2\frac{S_Y^2}{S_X^2} \right)\\ & F_1 = \frac{1}{f_{1-\alpha/2,n_Y-1,n_X-1}}\\ & F_2 = f_{1-\alpha/2,n_X-1,n_Y-1} \end{split} \tag{1.5} \end{equation}\]

Ejemplo 1.6 Utilizando la base de datos dolar.csv, elabore un intervalo de confianza para el cociente de la variabilidad del valor del dólar entre los meses de junio y julio, asumiendo que las distribuciones poblacionales son normales e independientes

Para estudiar o comparar varianzas, corresponde elaborar el único intervalo especificado en esta sección.

\[\left( F_1\frac{S_Y^2}{S_X^2},F_2\frac{S_Y^2}{S_X^2} \right)\]

La ejecución en R, considerando una confianza del 95% es la siguiente.

junio = df$Valor[df$Mes=="Junio"]
julio = df$Valor[df$Mes=="Julio"]
var.test(x = junio, y = julio, conf.level = 0.95)

## 
##  F test to compare two variances
## 
## data:  junio and julio
## F = 2.2409, num df = 19, denom df = 17, p-value = 0.1004
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.8510277 5.7522904
## sample estimates:
## ratio of variances 
##           2.240867

Dado que, la probabilidad asociada a este intervalo de confianza contiene al cociente de las varianzas poblacionales, para determinar si existe o no diferencia entre estos parámetros se debe verificar si el 1 está dentro o no del intervalo. En caso de que el 1 esté dentro del intervalo, entonces, se asume que las varianzas poblacionales son iguales.

En este sentido, el intervalo asociado al ejemplo es \((0.8, 5.7)\), el cual, contiene al 1. Por lo tanto, se asume que las varianzas del valor del dólar de ambos meses es igual, con un 95% de confianza.

Ejercicio 1.7 Considerando el ejercicio 1.4, elabore un intervalo de confianza para la comparación de varianzas de ambas poblaciones. Asuma, que las distribuciones poblacionales son normales e independientes. Utilice una confianza del 93.2%. Interprete.

Ejercicio 1.8 Utilizando la base de datos del Imacec, elabore un intervalo de confianza para comparar la variabilidad (varianza) del valor del Imacec entre ambos sectores. Asuma, que las distribuciones poblacionales son normales e independientes. Utilice una confianza del 90%. Interprete.

Ejercicio 1.9 Utilizando la base de datos del Imacec, elabore un intervalo de confianza para estudiar la diferencia la media del Imacec de ambos sectores. Asuma, que las distribuciones poblacionales son normales e independientes. Utilice una confianza del 92%. Interprete.

Ejercicio 1.10 Utilizando la base de datos del Imacec, elabore un intervalo de confianza para estudiar si, el promedio del Imacec de minería es mayor al de industria por más de 2 unidades. Asuma, que las distribuciones poblacionales son normales e independientes. Utilice una confianza del 97%. Interprete.

1.5 Ejercicios

A continuación, desarrolle los ejercicios manualmente sin el uso de R.

Ejercicio 1.11 Una empresa desea estimar el tiempo promedio de espera (en minutos) en un sistema de atención. Se sabe que la desviación estándar poblacional es \(\sigma = 2.0\) minutos. Se registraron los siguientes tiempos de espera: 18, 20, 17, 22, 19, 21, 20, 18, 19, 20. Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar el promedio poblacional de los tiempos de espera. Use que \(Z_{1-0.05/2} = 1.9599\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.12 Un investigador mide la satisfacción de clientes en una escala de 0 a 100 puntos. La varianza poblacional es desconocida. Se registraron los siguientes valores: 72, 75, 78, 70, 74, 80, 77, 73. Con un nivel de confianza del 99% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el promedio poblacional supera 75. Use que \(t_{1-0.01,\,7} = 2.9980\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.13 Dos métodos de producción (A y B) generan rendimientos (en unidades por hora). Se conocen las desviaciones estándar poblacionales: \(\sigma_A = 3.0\) y \(\sigma_B = 2.5\). Para el método A se obtuvieron los siguientes datos: 102, 100, 98, 101, 99, 100, 97, 103, 101, 98. Para el método B se obtuvieron los siguientes datos: 95, 97, 94, 96, 95, 93, 92, 94, 96. Con un nivel de confianza del 90% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si la media poblacional de A es mayor que la de B por menos de 6 unidades. Use que \(Z_{0.10} = 1.2816\). En su respuesta indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.14 Un equipo desea estimar el tiempo promedio (en minutos) de descarga de un archivo. Se conoce la desviación estándar poblacional \(\sigma = 1.5\). Se registraron los siguientes tiempos: 5.2, 4.8, 5.5, 5.1, 4.9, 5.3, 5.0, 5.4, 4.7, 5.2. Con un nivel de confianza del 99% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar el promedio poblacional de los tiempos de descarga. Use que \(Z_{1-0.01/2} = 2.5758\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.15 Una empresa monitorea el gasto promedio por compra (en miles de pesos). La varianza poblacional es desconocida. Se registraron los siguientes montos: 62, 68, 71, 65, 69, 70, 66, 64, 67. Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el gasto promedio poblacional es menor a 70. Use que \(t_{1-0.05,\,8} = 1.8331\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.16 Dos líneas de producción (A y B) registran rendimiento (unidades por hora). Se conocen las desviaciones estándar poblacionales: \(\sigma_A = 2.0\) y \(\sigma_B = 2.2\). Para A se observaron los siguientes valores: 48, 50, 49, 51, 52, 47, 50, 49, 51. Para B se observaron los siguientes valores: 45, 46, 47, 44, 46, 45, 47, 48. Con un nivel de confianza del 97% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el rendimiento promedio de A supera al de B por más de 3 unidades. Use que \(Z_{0.97} = 1.8808\). En su respuesta indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.17 Un servicio técnico registra la duración (en minutos) de reparaciones rápidas. Se conoce la desviación estándar poblacional \(\sigma = 3.0\). Se observaron los valores: 34, 29, 31, 33, 35, 30, 28, 32, 31, 34, 30. Con un nivel de confianza del 90% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar el promedio poblacional de la duración de las reparaciones. Use que \(Z_{0.95} = 1.6449\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.18 En una encuesta de satisfacción (0–100), la varianza poblacional es desconocida. Se registraron los siguientes puntajes: 81, 79, 85, 83, 80, 78, 82, 84, 81, 77. Con un nivel de confianza del 98% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el promedio poblacional supera 80. Use que \(t_{1-0.02,\,9} = 2.2622\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.19 Dos aplicaciones (A y B) miden el tiempo de respuesta (en milisegundos). Se conocen las desviaciones estándar poblacionales: \(\sigma_A = 12\) y \(\sigma_B = 10\). Para A se observaron: 210, 205, 198, 202, 207, 200, 203, 206, 199. Para B se observaron: 195, 197, 193, 198, 196, 194, 199, 192. Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el tiempo promedio de A es menor que el de B por menos de 8 ms. Use que \(Z_{0.95} = 1.6449\). En su respuesta indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.20 Una fintech registra el tiempo de aprobación de solicitudes (segundos). Se conoce la desviación estándar poblacional \(\sigma = 4.0\). Se observaron los valores: 52, 48, 50, 55, 53, 49, 51, 47, 54, 50. Con un nivel de confianza del 92% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar el promedio poblacional del tiempo de aprobación. Use que \(Z_{0.96} = 1.7507\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.21 Un banco evalúa el tiempo promedio de atención (minutos) y la varianza poblacional es desconocida. Se registraron los tiempos: 9.2, 10.1, 8.7, 9.5, 9.8, 10.3, 9.0, 9.6. Con un nivel de confianza del 90% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el tiempo promedio poblacional es menor a 10. Use que \(t_{1-0.10,\,7} = 1.4398\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.22 Dos campañas (A y B) reportan la tasa de clics (por mil impresiones). Se conocen las desviaciones estándar poblacionales: \(\sigma_A = 0.9\) y \(\sigma_B = 1.1\). Para A se registraron: 12.1, 11.8, 12.5, 12.0, 11.9, 12.3, 12.2, 11.7, 12.4. Para B se registraron: 10.8, 11.1, 10.9, 11.0, 10.7, 11.2, 10.6, 10.9. Con un nivel de confianza del 94% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si la tasa promedio de A supera a la de B por más de 1.0. Use que \(Z_{0.94} = 1.5548\). En su respuesta indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.23 Una fábrica mide el tiempo de ensamblaje de una pieza (minutos). Se conoce la desviación estándar poblacional \(\sigma = 2.5\). Se observaron los tiempos: 42, 45, 44, 46, 43, 41, 47, 44, 42, 45. Con un nivel de confianza del 90% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar el promedio poblacional del tiempo de ensamblaje. Use que \(Z_{0.95} = 1.6449\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.24 Una encuesta estudia el número de horas de uso de internet diario. La varianza poblacional es desconocida. Se registraron: 3.5, 4.0, 3.8, 4.2, 3.9, 4.1, 3.7, 3.6. Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el promedio poblacional es mayor a 3.8 horas. Use que \(t_{1-0.05,\,7} = 1.8946\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.25 Dos sucursales (A y B) reportan ingresos diarios (miles de pesos). Se conocen las desviaciones estándar poblacionales: \(\sigma_A = 4.0\) y \(\sigma_B = 3.5\). Para A se observaron los siguientes datos: 120, 118, 122, 121, 119, 117, 123. Para B se observaron los siguientes datos: 115, 116, 117, 114, 115, 116, 113. Con un nivel de confianza del 94% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el ingreso promedio de A supera al de B por más de 5 unidades. Use que \(Z_{0.94} = 1.5548\). En su respuesta indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.26 Se mide la duración de llamadas telefónicas (segundos). Se conoce la desviación estándar poblacional \(\sigma = 5.0\). Se registraron los valores: 101, 98, 100, 102, 97, 103, 99, 101, 100, 98. Con un nivel de confianza del 92% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar el promedio poblacional de la duración de llamadas. Use que \(Z_{0.96} = 1.7507\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.27 Un estudio mide el consumo de agua (litros/día). La varianza poblacional es desconocida. Se observaron: 2.3, 2.5, 2.4, 2.6, 2.2, 2.7, 2.5, 2.4, 2.6. Con un nivel de confianza del 97% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el consumo promedio poblacional es menor a 2.6. Use que \(t_{1-0.03,\,8} = 1.8946\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.28 Dos métodos de enseñanza (A y B) son evaluados con puntajes. Se conocen las desviaciones estándar poblacionales: \(\sigma_A = 5.0\) y \(\sigma_B = 4.5\). Para A se registraron: 78, 82, 80, 81, 79, 83, 80. Para B se registraron: 74, 76, 73, 75, 74, 72, 76. Con un nivel de confianza del 99% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el puntaje promedio de A es mayor que el de B por menos de 8 puntos. Use que \(Z_{0.99} = 2.3263\). En su respuesta indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.29 Un servicio de streaming mide el tiempo promedio de visualización de un episodio (minutos). Se conoce la desviación estándar poblacional \(\sigma = 6.0\). Se observaron: 42, 40, 41, 39, 44, 43, 41, 40, 42, 39. Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar el promedio poblacional del tiempo de visualización. Use que \(Z_{1-0.05/2} = 1.9599\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.30 Un estudio evalúa la cantidad de pasos diarios (en miles). La varianza poblacional es desconocida. Se observaron: 8.2, 7.9, 8.4, 8.1, 8.3, 8.0, 7.8, 8.2. Con un nivel de confianza del 90% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el promedio poblacional es mayor a 8.0. Use que \(t_{1-0.10,\,7} = 1.4398\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.31 Dos programas de ejercicio (A y B) registran reducción de peso (en kilogramos). Se conocen las desviaciones estándar poblacionales: \(\sigma_A = 1.5\) y \(\sigma_B = 1.2\). Para A se obtuvieron: 4.5, 5.0, 4.7, 4.9, 5.1, 4.8. Para B se obtuvieron: 3.9, 4.1, 4.0, 3.8, 4.2, 3.7. Con un nivel de confianza del 96% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si la reducción promedio de A es menor que la de B por menos de 1.0. Use que \(Z_{0.96} = 1.7507\). En su respuesta indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza utilizado y la interpretación en el contexto.

Ejercicio 1.32 Un analista financiero estudia el tiempo de espera (en minutos) en una plataforma de inversión. La desviación estándar poblacional es \(\sigma = 4.0\). Los tiempos registrados fueron: 18, 21, 19, 22, 20, 23, 19, 21, 20, 22. Con un nivel de confianza del 90% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar el promedio poblacional de los tiempos de espera. Use que \(Z_{1-0.10/2} = 1.6449\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.33 Una empresa de transporte desea evaluar el tiempo promedio de entrega (en horas) de pedidos. La varianza poblacional es desconocida. Se observaron: 12, 11, 10, 13, 12, 14, 11, 12. Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el promedio poblacional de entrega es menor a 13. Use que \(t_{1-0.05,\,7} = 1.8946\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.34 Un banco analiza el gasto promedio mensual (en miles de pesos) de sus clientes. La varianza poblacional es desconocida. Los datos son: 450, 470, 465, 480, 455, 475, 460, 470. Con un nivel de confianza del 97% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el gasto promedio poblacional es mayor a 460. Use que \(t_{1-0.03,\,7} = 2.3650\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.35 Dos grupos de estudiantes (A y B) rinden un test de matemáticas. Se conocen las varianzas poblacionales: \(\sigma_A^2 = 25,\ \sigma_B^2 = 16\). Grupo A: 72, 75, 70, 74, 71, 76, 73, 72, 74. Grupo B: 68, 65, 70, 66, 67, 69, 68, 70. Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si la media poblacional de A supera a la de B en más de 2 puntos. Use que \(Z_{0.95} = 1.6449\). En su respuesta indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.36 Un investigador compara el rendimiento promedio de dos procesos (A y B). La varianza poblacional es desconocida pero se asume igual en ambos grupos. A: 102, 105, 100, 104, 101, 103, 106. B: 98, 95, 99, 97, 96, 100, 94. Con un nivel de confianza del 90% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el rendimiento promedio de A es mayor al de B por menos de 7 puntos. Use que \(t_{1-0.10,\,12} = 1.3562\). En su respuesta indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.37 Dos métodos de cultivo (A y B) se comparan en rendimiento (kg). La varianza poblacional es desconocida y no se asume igual. A: 210, 215, 220, 212, 218, 214. B: 200, 205, 198, 202, 199, 203. Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si la diferencia promedio poblacional entre A y B es menor a 15. Use que \(t_{1-0.05,\,13}=2.2281\). En su respuesta indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.38 Un fabricante analiza la variabilidad en el tiempo de carga de baterías (minutos) entre dos modelos A y B. Los tiempos fueron: A: 120, 118, 122, 121, 119, 117, 123, 120. B: 115, 116, 114, 117, 115, 113, 118, 116. Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para comparar la razón de varianzas poblacionales \(\sigma_A^2/\sigma_B^2\). Use que \(F_{1-0.05/2,\,7,\,7} = 4.99\) y \(F_{0.05/2,\,7,\,7} = 0.20\). Indique los parámetros en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.39 Un estudio mide la variabilidad en los tiempos de reacción (segundos) entre dos grupos de deportistas A y B. A: 0.45, 0.47, 0.46, 0.44, 0.48, 0.45, 0.47. B: 0.42, 0.40, 0.43, 0.41, 0.44, 0.42, 0.43. Con un nivel de confianza del 90% y asumiendo normalidad de los datos, elabore un intervalo de confianza para comparar la razón de varianzas poblacionales \(\sigma_A^2/\sigma_B^2\). Use que \(F_{1-0.10/2,\,6,\,6} = 3.87\) y \(F_{0.10/2,\,6,\,6} = 0.26\). Indique los parámetros en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.40 Un laboratorio mide la concentración de un reactivo (mg/L) en 8 muestras. Valores: 52, 55, 54, 56, 53, 57, 55, 54. Con un nivel de confianza del 90% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si la concentración promedio poblacional es mayor a 53. Use que \(t_{1-0.10,\,7} = 1.4149\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.41 Una encuesta registra la cantidad de horas de estudio semanal de un grupo de estudiantes: 8, 10, 9, 11, 10, 12, 9, 10. La desviación estándar poblacional es \(\sigma = 1.5\). Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar el promedio poblacional de horas de estudio. Use que \(Z_{1-0.05/2} = 1.9599\). En su respuesta indique la media poblacional en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.42 Dos equipos de ventas (X e Y) registran el número de contratos cerrados en una semana. Se asume que las varianzas poblacionales son iguales. X: 15, 18, 16, 17, 19, 20, 18. Y: 12, 14, 13, 15, 14, 13, 12. Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el promedio poblacional de X supera al de Y en más de 3 contratos. Use que \(t_{1-0.05,\,12} = 1.7823\). Indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.43 Un investigador mide la presión arterial en dos grupos de pacientes (Tratamiento y Control) bajo distintas dietas. Se asume que las varianzas poblacionales son iguales. Tratamiento: 122, 125, 128, 124, 126, 127. Control: 118, 117, 120, 119, 121, 118. Con un nivel de confianza del 90% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si la diferencia promedio poblacional entre los grupos es menor a 10 mmHg. Use que \(t_{1-0.10,\,10} = 1.3722\). Indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.44 Dos cursos (Ingeniería e Economía) rinden un examen de cálculo. Se asume que las varianzas poblacionales son iguales. Ingeniería: 72, 75, 73, 74, 76, 71, 75. Economía: 68, 70, 69, 67, 71, 68, 70. Con un nivel de confianza del 92% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si la media de Ingeniería es mayor que la de Economía por más de 5 puntos. Use que \(t_{1-0.08,\,12} = 1.4353\). Indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.45 Una empresa compara la productividad (unidades por hora) en dos plantas (Planta 1 y Planta 2). Se asume que las varianzas poblacionales son iguales. Planta 1: 105, 110, 108, 107, 109, 106. Planta 2: 100, 98, 101, 99, 102, 100. Con un nivel de confianza del 97% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si la productividad promedio de Planta 1 supera a la de Planta 2 en menos de 10 unidades. Use que \(t_{1-0.03,\,10} = 2.2281\). Indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.46 Un laboratorio compara los niveles de glucosa en dos grupos de pacientes (X e Y) tras un tratamiento. No se asume igualdad de varianzas poblacionales. X: 92, 95, 94, 96, 93, 97. Y: 88, 85, 90, 87, 89, 86. Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si el promedio poblacional de X es mayor al de Y en más de 6 unidades. Use que \(t_{1-0.05,\,10} = 2.2281\). Indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.47 Dos procesos de manufactura (Proceso 1 y Proceso 2) se comparan en defectos por lote. No se asume igualdad de varianzas poblacionales. Proceso 1: 12, 14, 13, 15, 14. Proceso 2: 9, 10, 8, 11, 9. Con un nivel de confianza del 90% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si la diferencia promedio poblacional de defectos es menor a 7. Use que \(t_{1-0.10,\,7} = 1.8946\). Indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.48 Un investigador mide el tiempo de reacción (ms) en dos grupos (Grupo Control y Grupo Experimental). No se asume igualdad de varianzas poblacionales. Grupo Control: 220, 225, 218, 222, 219. Grupo Experimental: 210, 212, 208, 211, 209. Con un nivel de confianza del 92% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si la media poblacional del Grupo Control supera a la del Grupo Experimental en menos de 15 ms. Use que \(t_{1-0.08,\,8} = 1.8595\). Indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.49 Dos métodos de entrenamiento físico (Método A y Método B) se comparan en la reducción de tiempo en una carrera (segundos). No se asume igualdad de varianzas poblacionales. Método A: 62, 65, 63, 64, 66. Método B: 58, 57, 59, 56, 60. Con un nivel de confianza del 97% y asumiendo normalidad de los datos, elabore un intervalo de confianza para estudiar si la diferencia promedio de reducción es mayor a 3 segundos. Use que \(t_{1-0.03,\,7} = 2.3650\). Indique las medias poblacionales en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.50 Un estudio analiza la variabilidad de los salarios en dos áreas de una empresa (Área Técnica y Área Administrativa). Área Técnica: 1200, 1250, 1230, 1240, 1260, 1220. Área Administrativa: 1180, 1170, 1160, 1190, 1185, 1175. Con un nivel de confianza del 95% y asumiendo normalidad de los datos, elabore un intervalo de confianza para comparar la razón de varianzas poblacionales \(\sigma^2_{\text{Técnica}}/\sigma^2_{\text{Administrativa}}\). Use que \(F_{1-0.05/2,\,5,\,5} = 5.05\) y \(F_{0.05/2,\,5,\,5} = 0.20\). Indique los parámetros en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Ejercicio 1.51 Un análisis compara la variabilidad en el tiempo de entrega de dos proveedores (Proveedor X y Proveedor Y). Proveedor X: 32, 34, 33, 35, 31, 36. Proveedor Y: 28, 29, 30, 27, 31, 29. Con un nivel de confianza del 90% y asumiendo normalidad de los datos, elabore un intervalo de confianza para comparar la razón de varianzas poblacionales \(\sigma^2_{X}/\sigma^2_{Y}\). Use que \(F_{1-0.10/2,\,5,\,5} = 3.97\) y \(F_{0.10/2,\,5,\,5} = 0.25\). Indique los parámetros en estudio, el tipo de intervalo, el nivel de confianza y la interpretación en el contexto.

Referencias

Anderson, D. R., Sweeney, D. J., & Williams, T. A. (2008). Estadística para administración y economía (10a ed). Cengage Learning.

Devore, J. L. (2008). Probability and statistics for engineering and the sciences (7th ed). Thomson/Brooks/Cole.